시계열 데이터 분석에서의 어려움
- 현존 하는 데이터 증강 기법들은 시계열 데이터의 내제적 특성(intrinsic property)을 활용하지 못함
- 일반적으로 시계열 데이터는 시간 종속성(Temporal Dependency)라는 특성을 가지고 있음
- 이미지나 언어 데이터와 다르게 시계열 데이터는 크게 시간(time)과 빈도(Frequency) 도메인으로 나눌 수 있는데, 이러한 각각의 transformed domain에 적합한 데이터 증강이 수행되어야 하기 때문에 다른 데이터에 비해 비교적 어려움
- 현존하는 데이터 증강 기법들은 task에 의존적인 경향이 존재함
- time Series Classification에 쓰인 증강기법이, time Seriese Anomaly Detection에는 적합하지 않을 수 있음
- 데이터 간의 불균형이 큰 데이터와 그렇지 않은 데이터를 활용함에 있어서 다른 접근의 data Augmentation이 필요할 수 있음


-> 모든 Task에 있어서 데이터 증강을 수행한 모델의 성능이 가장 좋은 것을 확인 할 수 있음
Basic Data Augmentation




Fourier Transform(푸리에 변환)
- 일반적으로 시계열 데이터는 여러 종류의 Sin, Cos파장들로 이루어져 있음
- 푸리에 변환은 신호의 주파수 (Frequency)분석을 수행할 때 사용되며, time Domain을 Frequency Domain으로 변환해줌

Frequency Domain Data Augmentation
🧐🧐🧐🧐🧐🧐🧐🧐🧐🧐
* APP(Amplitude and Phase Perturbations)
- 앞에서 소개한 시계열 데이터의 Amplitude Spectrum과 Phase Spectrum에 Perturbation을 수행한 방법
- 1) Amplityde Spectrum: 일부 데이터를 원본 데이터의 평균과 분산을 갖는 Gaussian Noise로 대체함
- 2) Phase Spectrum: 일부 데이터에 zero-mean Gaussian Noise를 더해줌
* AAFT (Amplitude Adjusted Fourier Transform) & IAAFT(iterated AAFT)
- AAFT는 Fourier Transform 후 Phase Spectrum 에서 무작위로 Phase를 Shuffle한 뒤 Inverse Fourier Transform을 수행하여 Amplitude는 보존되고 Phase만 바뀐 데이터를 생성하는 방법
- IAAFT는 AAFT의 발전된 버전으로, iterative step을 통해 AAFT가 좀 더 잘 수렴할 수 있도록 개선 시키는 방법
- AAFT 및 IAAFT를 통해 생성된 시계열은 대략적을 기존 시계열 데이터의 시간 상관 관계, 전력 스펙트럼 및 진폭 분포 보존이 가능함
Time-Frequency Domain Data Augmentation
* STFT (short Term Fourier Transform)
- STFT는 주파수 특성이 시간에 따라 달라지는 특성을 분석하기 위한 방법
- 시계열 데이터를 시간 단위로 짧게 쪼개서 FFT를 수행하는 방법
- 차용 데이터 증강 기법 1) local Averaging 수행 2) feature vector들의 shuffling 수행
* Mel spectrogram

- 주파수의 단위를 위 공식에 따라 멜 단위(mel unit)로 바꾼 스펙트럼을 일컬음
- 청각이 저음의 주파수 변화에 민감하고 고음의 주파수 변화에 덜 민감한 특징을 반영함
- 차용 데이터 증강 기법 1) Warping Features수행 2) Masking Blocks of Frequency(or Time) 수행
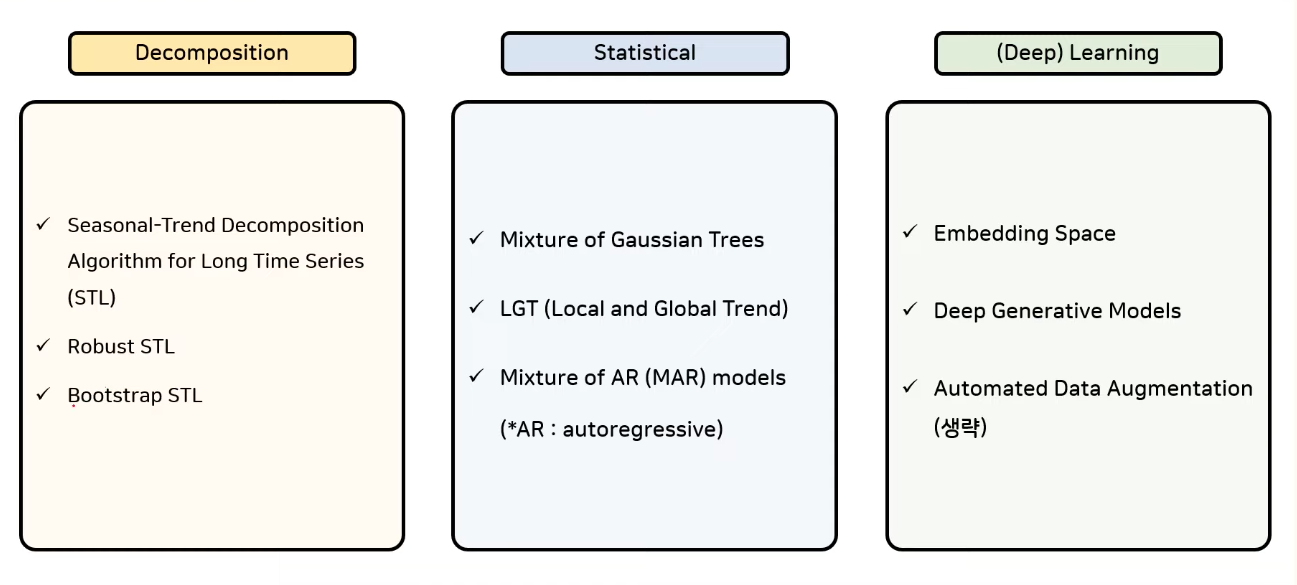
Advanced Data Augmentation


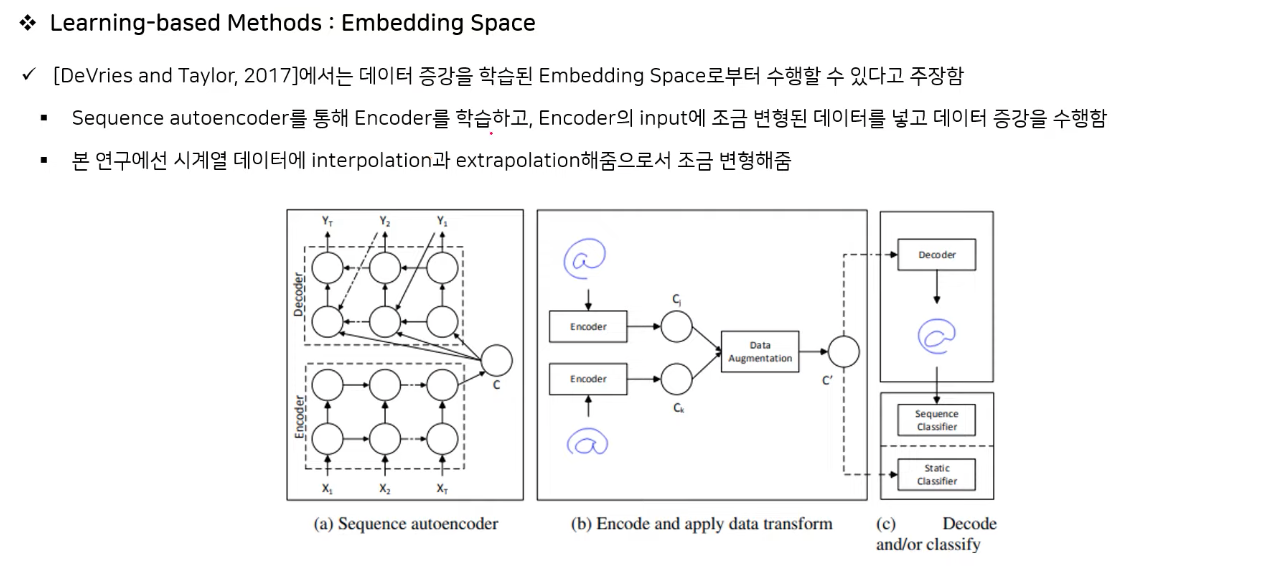

'ReinforcementLearning' 카테고리의 다른 글
| [paper]Dense Passage Retrieval for open-Domain Questionestions and passages Answering(2020) (0) | 2023.04.06 |
|---|---|
| [논문리뷰]Diversity is all you need: Learning skills without a reward function (0) | 2023.04.03 |
| meta-learning + RL (0) | 2023.04.03 |
| 계층적 강화 학습이란? (0) | 2023.04.03 |
| [ppo]Proximal policy optimization algorithms (0) | 2023.04.03 |
